The Bit That I Don't Like About D20

"And Thorpe makes the turn in the lead... Ian Thorpe is heading for an Olympic gold... no, he seems to have forgotten how to swim... he's sinking... and who's that on the outside lane..? It's Eric the Eel, he's in the lead..."

Now in a "heroic" game it's fine for the Finnish World Champion to roll a one, and only make it fifty metres off the end of the ski-jump ramp, only to watch as Eddie the Eagle rolls a twenty and flies a hundred and twenty metres to the gold medal.

But real life isn't like that.

Which is basically why I have problems with the idea of using D20 for non-heroic games.

Before I continue, I should point out that what I'm about to say is in no way original. I've seen dozens of people on various message forums say that they don't like D20 because it has a poor probability curve. But they never explain what they mean by that, and it occurred to me that people who haven't, as I have, studied Statistics (I failed it at A level, and hence have partial knowledge of it) might not have any idea what they mean by "probability curve".

So I figured I might as well try to explain, just so that we all know what we're arguing about. (And if some of you already know this, and figure I'm being patronising... fuck off!)

To do this, I'm going to use two dice rolling mechanisms, both simplified versions of ones used in actual games. The first is, of course, D20. You roll a D20, add your skill to it, and it must be equal to, or higher than, a difficulty number. If you roll a 1 you have automatically failed. If you roll a 20 you have automatically succeeded.

The second system is based on the one that Steve Jackson Game's GURPS {http://www.sjgames.com/gurps/} uses. In this one, you roll three six-sided dice, add them together, and then add your skill on. The total must equal or exceed a difficulty number. If you roll 3 (three ones) you have automatically failed. If you roll 18 (three sixes) you have automatically succeeded.

Firstly, what do we mean by a probability curve?

Well imagine if you did a bar graph showing how likely you were to roll a particular number on a D20. It would be flat, since you have an exactly 5% (one in twenty) chance of rolling each number.

But if you did the same with the second method (3D6) you would get a bell-shaped curve (what they call a bell curve) like the diagram below shows:

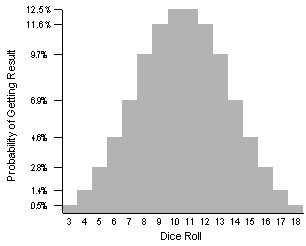
With 3D6, you have a 12.5% chance of rolling a 10, but only a 0.5% chance of rolling an 18 or a 3 (actually it's 0.46%, just to stop people nit-picking). If you're wondering why this is, it's because there are many different ways of rolling 10 on 3D6 (6+2+2, 6+3+1, 6+1+3, 5+2+3 etc.) but there is only a single way of rolling a 3 or an 18 (1+1+1 and 6+6+6).

But what does this actually mean, and more importantly - why does it matter?

Okay, let's use our two methods to resolve a particular test. Let's say that it's navigating a canoe down a white-water river using a "canoe" skill.

We have three blokes, Andy, Barry and Charlie. Andy is a novice at canoing, so we'll give him a skill of 0. Barry is at an intermedate level, so we'll give him a skill of 5. But Charlie is an expert at international standard, so we'll give him a skill of 10.

And we're going to send them down four rivers, rated easy, moderate, hard and very hard and see if they get to the end without capsizing. We give these four rivers difficulty ratings (the number you must equal or exceed) of 6, 11, 16 and 21.

How do they get on?

Here are their chances of success with the "D20" method:

Andy Barry Charlie

Easy 75% 95% 95%

Moderate 50% 75% 95%

Hard 25% 50% 75%

Very Hard 5% 25% 50%

Let's look at some of the implications of that table.

Firstly, even on the easy run there is still a significant (5%) chance for both Barry and Charlie to fail, which seems especially unfair if Charlie is supposed to be an expert. After all, even Andy only has a 25% chance of failure. So for ever five runs on the easy river that Andy muffs it, Charlie will screw up once.

Let's look at the hard run. This is so hard that an international standard expert like Charlie has a 1 in 4 chance of capsizing. And yet it is also so easy that a complete novice like Andy has a 1 in 4 chance of making it down without capsizing. In fact, there is a 1 in 16 chance that Andy will make it down on a run where Charlie capsizes.

(Now do you understand my bit about Ian Thorpe and Eric the Eel?)

And when you move to very hard, you find that although Charlie is more likely to make it than Barry (50% against 25%) it's not as though he's on a different level of ability. Barry isn't going to watch him in action and think: "that guys just on a different planet to me..."

I could go on, but I think you get the drift. This dice mechanism fails to handle wide ranges of ability, and is essentially too random. Yes, you can give people high or low levels of skill. But sooner or later, you end up with either "fail unless you roll 20" or "succeed unless you roll 1" in which case it hardly matters whether you have +15 or +25.

So, how well does our "3D6" mechanism handle it? Here are the chances:

Andy Barry Charlie

Easy 95.3% 99.5% 99.5%

Moderate 50% 95.3% 99.5%

Hard 4.7% 50% 95.3%

Very Hard 0.5% 4.7% 50%

Well, Andy is pretty good on the easy and moderate rivers, but is pretty hopeless on the hard and very hard ones. Meanwhile, Barry and Charlie are pretty similar on the easy and moderate rivers, without much chance of them screwing up, but on the hard and very hard ones, Charlie's superior skill becomes very apparent.

Which is why I think that this sort of dice mechanism is better for "realistic", skill based games. If I'm playing a space pilot with twenty years of experience, and I'm racing against someone with two hours of training, I should beat them *nearly* every time. Yeah, there is a very slight chance that I might make a mistake, but it should be pretty damn unlikely.

Contents...